240808
1. 문자열 계산식
- 문자열 수식 계산의 일반적 방법 :1. 중위표현식 2. 하위 표현식(연산자를 피연산자 뒤에 쓰는 연산 표기법)
3 + 5 × 2 # 중위표기법
352*+ # 하위표기법
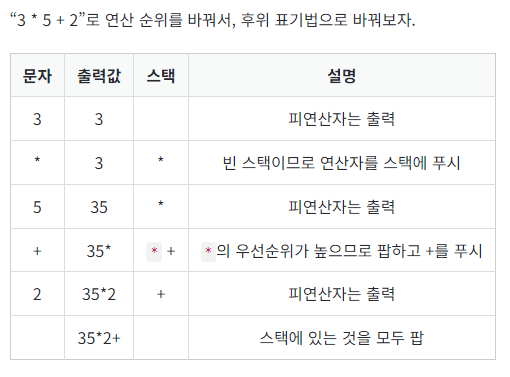
3*5+2 #중위표기법
35*2+ #하위표기법
- 스택을 이용한 중위표현식 -> 하위표현식으로의 변환
- 왜 변환 해야할까? 컴퓨터의 효율성 측면
- 계산방식 : 참고함 https://wikidocs.net/192124
1) 문자열 수식을 순회한다.
2) 피연산자를 만나면 출력
3) 연산자를 만나면 연산자 스택에 연산자가 있는지 확인한다, 스택의 마지막 연산자가 현재 연산자보다 우선순위 높으면 pop 후 출력
4) 현재 연산자를 연산자 스택에 push
5) 순회를 다 마치고, 연산자 스택이 빌 때까지 pop하여 출력한다
참고로 *,/가 +,- 보다 우선순위가 높다.

여기서 잠깐! 만약 (짝이 맞는) 괄호가 있다면?
=> *보다 괄호의 우선순위가 높다
=> 오른쪽 괄호가 나오면 스택에서 왼쪽 괄호가 나올 때까지 출력
내가 한번 풀어봤다!
#아이디어 <핵심 : 후위표기법의 핵심은 피연산자뒤 연산자를 두는 것>
#1. stack 배열 생성
#2. 문자열를 순회한다
# - 피연산자면 우선 출력 str 다 담는다
# - 연산자이고, 연산자 stack에 비어있으면 담는다
# - 연산자이고, 연산자 stack이 비어있지 않으면, 연산자 stack에 담긴 최근 연산자와 우선순위를 비교한다
# -- 우선순위 : *, / > +, - : 코드 어떻게 구현? 파이썬에 혹시 내장? Nope! 딕셔너리로 내가 정의
# -- 연산자 stack에 담긴 연산자가 순회한 연산자보다 우선순위가 높으면, 연산자 stack에 담긴 최근 연산자 pop 후 출력
# --- 왜 pop 해주는 거지 -> '우선순위가 높은 애부터 먼저 계산을 해주려고' !!
# -- 연산자 stack에 현재 순회 연산자 push
# - 순회를 다 마치고, 연산자 스택이 빌때까지 pop하여 출력
T = int(input())
for tc in range(1,T+1):
str_input = input()
output = '' #출력 변수 #string 형식! 잊지말자
operator = [] #연산자 스택
#처리 사전 정의
dct = {'+':1, '-':1, '*':2 ,'/':2}
#문자열 순회
for s in str_input:
if s not in dct: #피연산자면
output= output + s
elif s in dct and not operator: #연사자이고 연산자 스택이 비어있으면
operator.append(s) #해당 연산자 push
else: #연산자이고 연산자 스택이 비어있지 않다면
if dct[operator[-1]] >= dct[s] : #현재 연산자보다 최근 스택에 담긴 연산자가 우선순위 높으면
recent_oper = operator.pop() #최근 연산자 pop
output = output + recent_oper # 출력
operator.append(s) # 현재 연산자 push
# 우선순위 낮으면 어떻게 처리해? 저장해!
else: operator.append(s)
#순회 다 마치고 연산자 스택 빌때까지 pop해서 계산
while operator:
recent_oper = operator.pop()
output = output + recent_oper
print(f'#{tc} {output}')
2. 백트래킹(A형 필수 출제❤)
1) 개념
- 백트래킹 기법 : 해를 찾는 도중에 막히면(즉, 해가 아니면) 되돌아가서 다시 해를 찾아가는 기법
- 최적화 문제와 결정 문제를 해결할 수 있다
- 결정문제란 문제의 조건을 만족하는 해가 존재하는지의 여부를 yes, no로 답하는 문제 -> swea 미로 찾기, 부분 집합의 합 문제 등
- 어떤 노도의 유망성 점검 후 유망하지 않다고 결정되면, 그 노드의 부모로 돌아가 다음 자식 노드로 감(가지치기)
- 시간복잡도 : O(b^d) -> b 각 노드에서의 분기 수(가능한 선택의 수), d 트리의 최대 탐색 깊이
2) 그럼 dfs와의 차이는?
- 어떤 노드에서 출발하는 경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음(가지치기)
- 즉 dfs는 모든 경로를 추적하는데 비해 백트래킹은 불필요한 경로를 조기에 차단
- 그러나 역시 최악의 경우 여전히 지수함수 시간을 요하므로 처리 불가능
3) 알고리즘에 적용하면
- dfs로 깊이 우선 탐색
- 유망한가를 보고, 유망하지 않으면 다른 자식 노드 탐색
#일반화 코드
def backtracking(현재상태 currentState) :
#종료 조건
if (currentState가 해답이면) :
해답 출력 또는 저장
return
#가능한 해 탐색
for (모든 가능한 선택 nextChoice) :
if (nextChoice가 유효하면) : #가지 치기
currentState에 nextChoice를 적용 #각 선택 경우에 따른 상태 업데이트
backtracking(새로운상태) #새로운 탐색
nextChoice 적용 취소 # 상태 되돌리기 : 다음 탐색에 영향을 주지 않기 위함(새로운 상태가 다음 탐색에 영향을 주는 경우만 적용)
#일반화코드에선 nextchoice 적용 취소 코드가 필요!!!!!!!!!!!
'SSAFY' 카테고리의 다른 글
| [수업기록] 알고리즘 : string(2) (0) | 2024.08.13 |
|---|---|
| [수업기록] 알고리즘 : stack(3) - 백트래킹(2) (0) | 2024.08.09 |
| [수업기록] 알고리즘 : stack (0) | 2024.08.06 |
| [수업기록] 알고리즘 : string (0) | 2024.08.02 |
| [수업기록] 알고리즘 : list(검색, 선택 정렬) (0) | 2024.08.01 |

