2023.07.15 빅리더 이상화 교수님 수업#1❤️
선형대수란?
1. 3가지 (선형) 연립 방정식을 푸는 것 ⭐⭐⭐
square system 미지수 개수 = 식의 개수(#넘버링) (해 1개)
unconstrained system 미지수 > 식 (해 무한히 많다)
over-constrained system 미지수 < 식 (등식을 만족하는 해가 거의 없다)
- least square, projection
2. 판별식
3. 벡터 공간 ⭐⭐⭐
연산에 의해 닫혀있는 공간(space), 집합
벡터라는 값의 공간
* 함수 공간 : function space
Basis 액션, 최소한의 핵심 벡터 (유니크하지 않다, 무한히 구할 수 있음..(?))
4. 특이값 분해 (고유값, 고유 벡터)
선형이란? Linearity
1. super position 파형 (중첩의 원리) Point 최소화해도 데이터 학습에 영향이 없다(만개의 데이터 - > 100개의 데이터)
f(x1+x2) = f(x1) + f(x2)
ex : 두 사람이 각자의 마이크로 소리를 스피커(출력)로 내보낼 때
2. Homogeniety
f(ax) = a * f(x)
Point a가 정수라면 super position과 같은 의미를 가진다. 정수가 아닌 경우, 값을 늘리던 줄이던 스케일링 한다면
출력값에도 그만큼 적용된다.
⭐즉 선형이란 = > f(ax1+bx2) = af(x1) + bf(x2)
선형의 예시 Examples of Linearity
1. 행렬(대표적 예시)
* 행렬 곱셈 Matrix multiplication
Ax1 + Ax2 = A(x1+x2)
2. y = mx + b (b=0) 라는 관계 (y 와 x 는 비례하다) ⭐ ⭐ ⭐
Point 아무 직선이나 선형이 아니다!
Point 선형이 성립되려면 원점을 지나야 한다!
3. 미적분 (대표적 예시)
*미적분은 함수가 아니라 연산하는 방법이다
4. AM Radio 시스템도 선형!
목소리 신호(파동 생성)에 대해 굉장히 촘촘하게 코싸인 함수를 곱함(진폭이란 부분을 생성)
신호가 공중으로 출력이 됨
다시 안테나로 원래의 목소리로 복원해서 송출
= 다수의 목소리가 하나로 합쳐져 우리가 듣게 됨
*FM Radio는 선형이 아님
벡터란 ? Vector
행렬과 비슷하게 생겼지만 다른 점은 열이 1개만 있음(한줄로만 표기)
즉 일렬로 나열할 수 있는 모든 데이터 구조
n차원 벡터 생김새 :
x = [ x1
x2
x3
..
xn ]
벡타의 내적 vector inner projection
내적 : 하나의 연산으로 두 벡터간의 길이(norm), 각도, 관계(유사성)을 말하는 것
span : (basis는) '백터 공간을 span 한다(구성한다)'
basis : 최소한의 (독립) 벡터들의 집합
벡터 공간이란?
closed set (연산 결과가 그 집합 안 원소가 되는 것)
조건
1. x + y = y + x 가 V라는 원소의 집합이라 하면
x, y 도 그렇다
2. k, x 도 (스칼라) V라는 원소의 집합이다
*스칼라란? 크기만 갖는 개념 <-> 벡터 : 크기, 방향 둘다 갖는

벡터 : 속도, 무게 등
matrix(행렬), vector

*어머나 아래 값에서 array 안의 알파 베타 표기는 지워야해!(양쪽으로 빼줌)
가우스 소거법( Point 연립방정식과 동일하다!)
1) 연립방정식 예시
2u+v+w =5 #1
4u-6v = -2 #2
-2u +7v +2w = 9 #3
#2 - 2*#1
#3-(-1)*#1
2) 역행렬
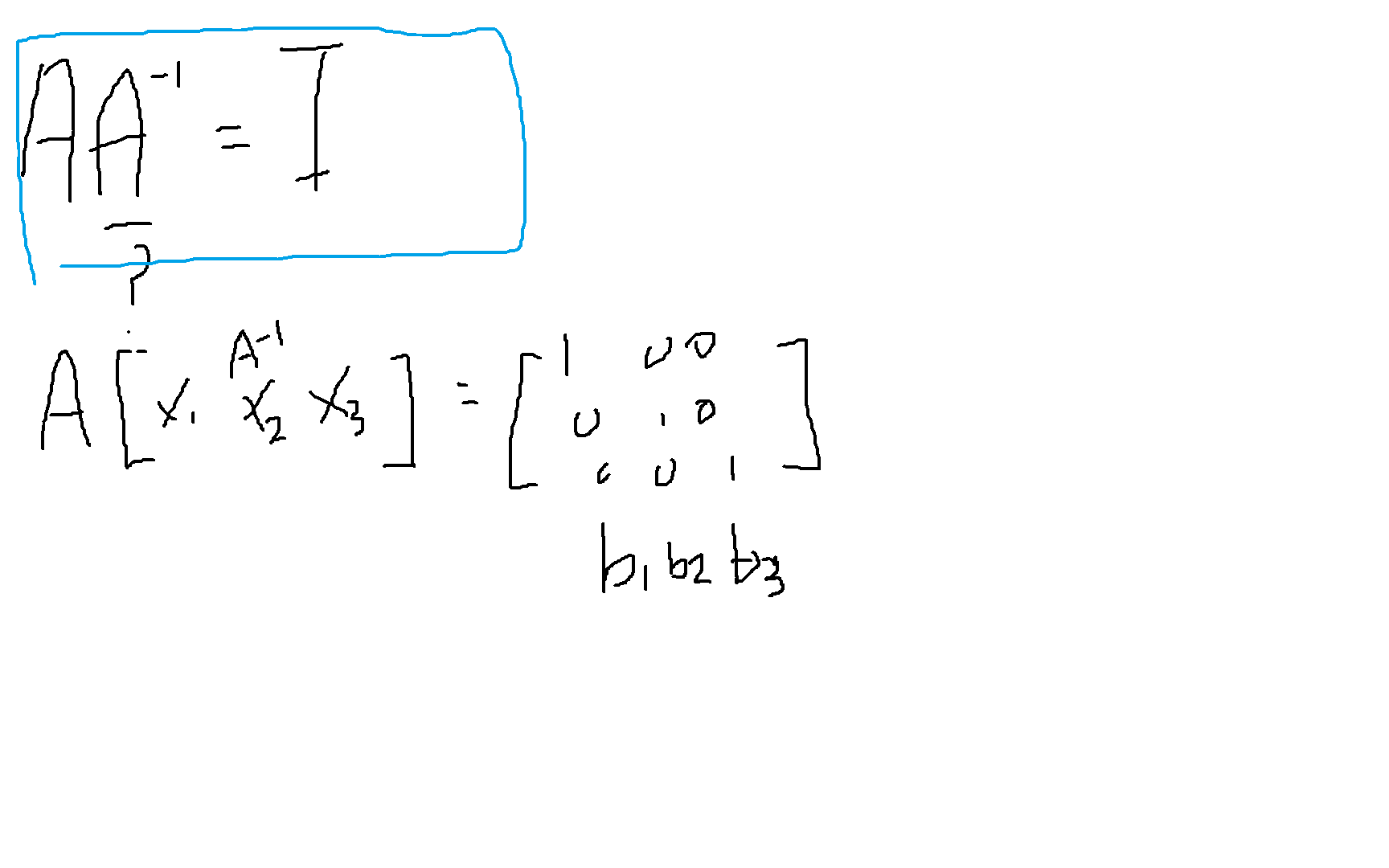
+
3*3 행렬
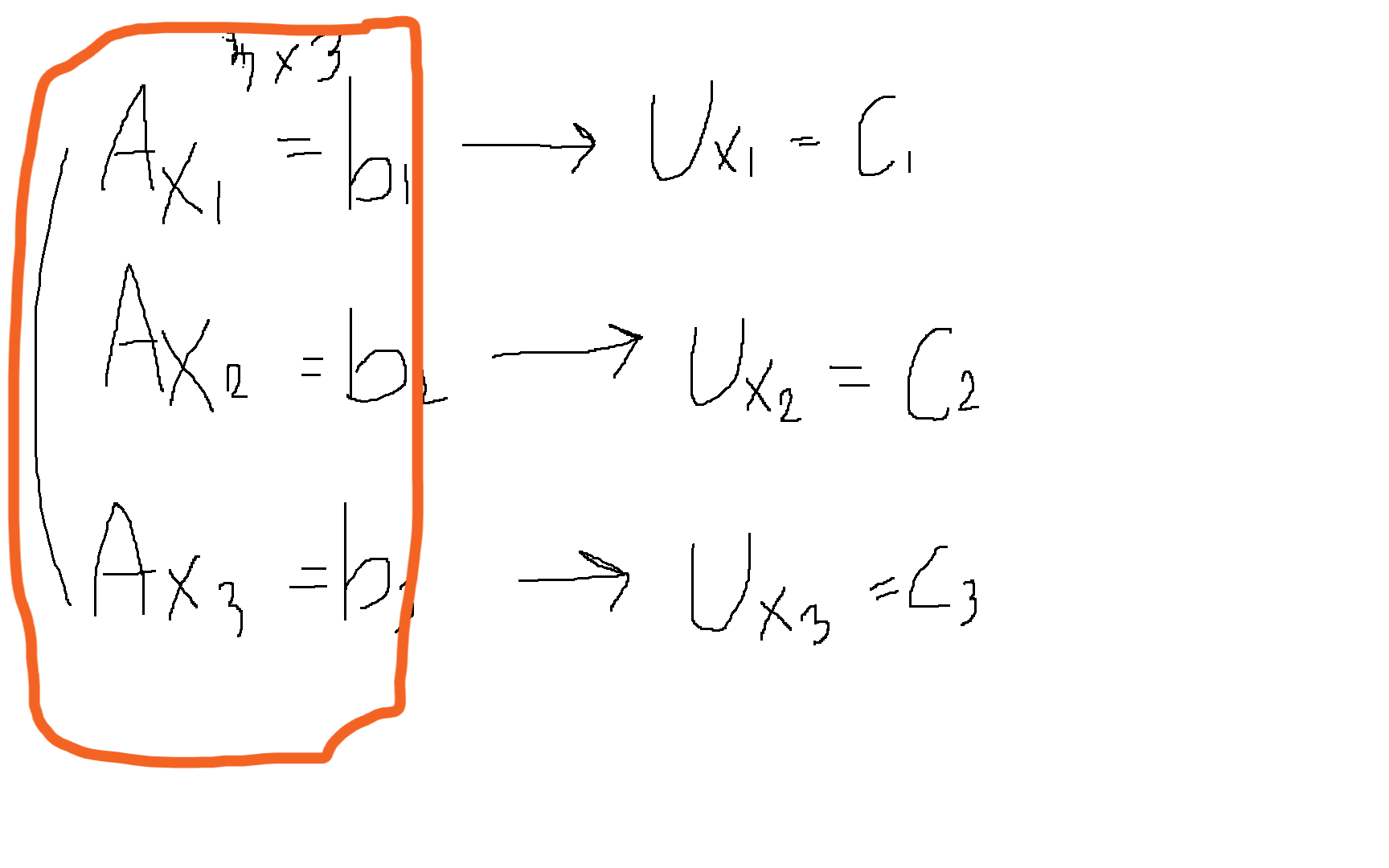
위 아래 주황색 영역은 서로 같은 값
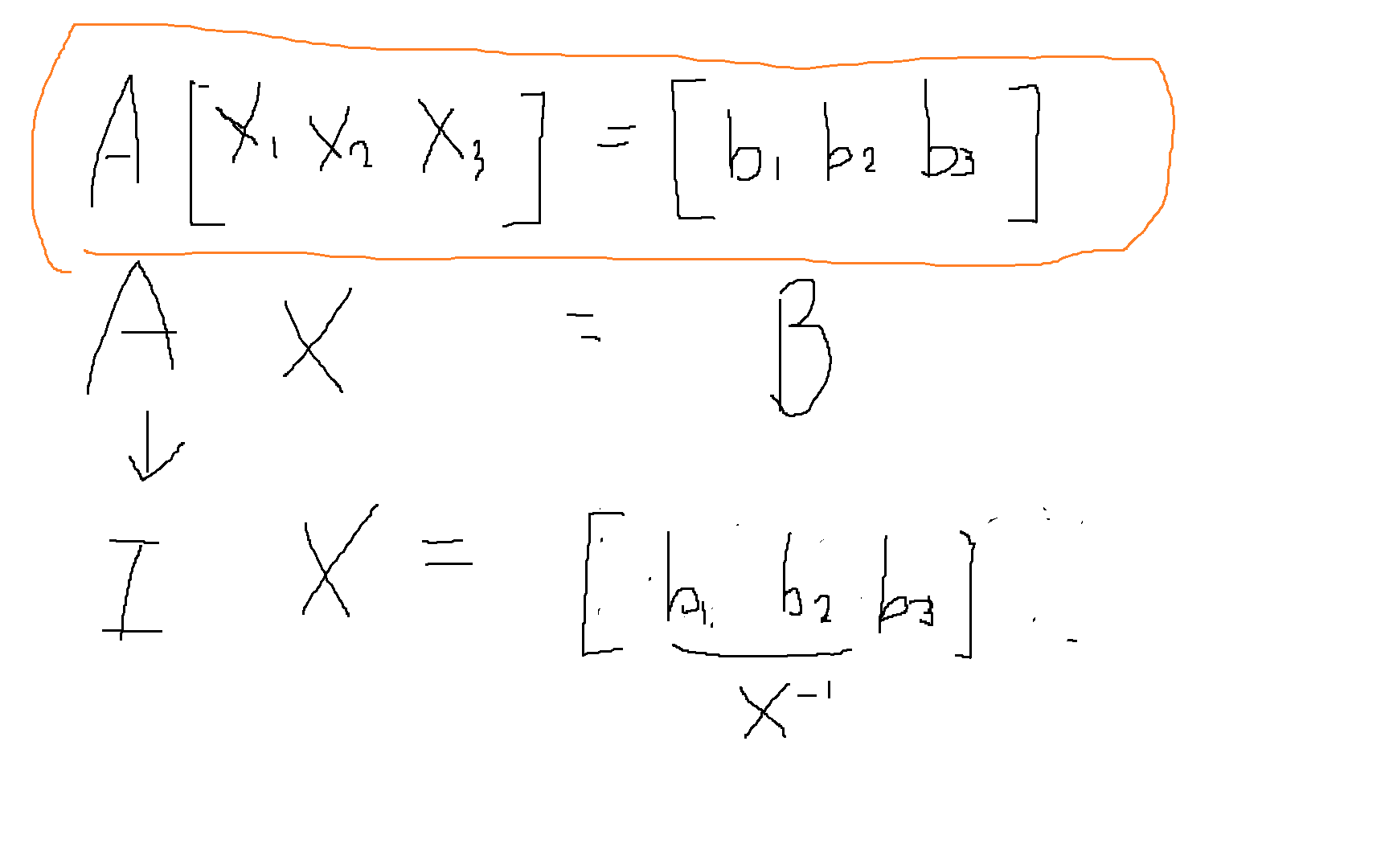
+
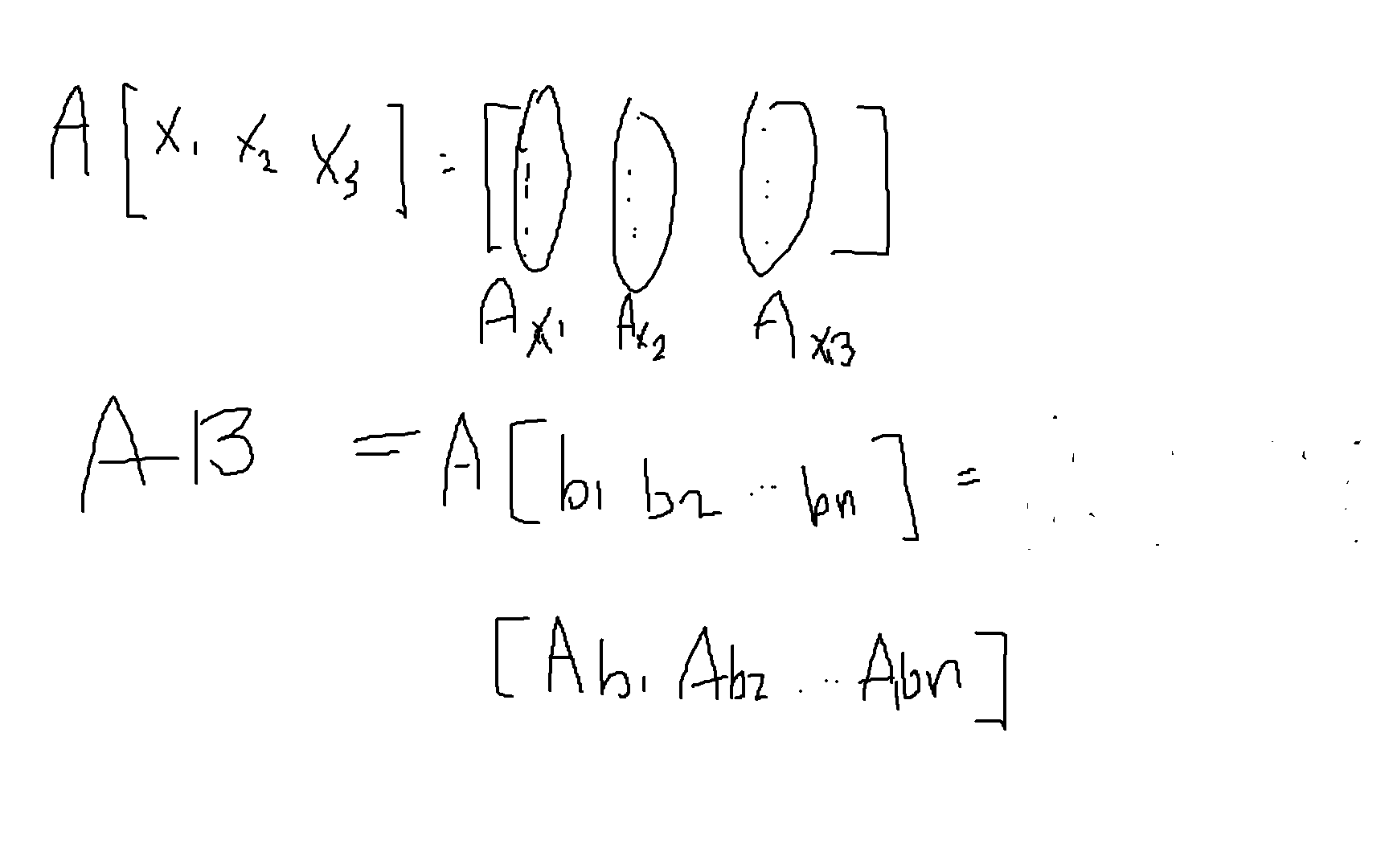
'선형대수' 카테고리의 다른 글
| 선형조합, 선형독립, 선형종속, 차원축소 (0) | 2023.08.28 |
|---|---|
| 벡터 공간, subspace, null space (0) | 2023.08.11 |
